A Probabilistic Formulation of LiDAR Mapping With Neural Radiance Fields
In this paper we reexamine the process through which a Neural Radiance Field (NeRF) can be trained to produce novel LiDAR views of a scene. Unlike image applications where camera pixels integrate light over time, LiDAR pulses arrive at specific times. As such, multiple LiDAR returns are possible for any given detector and the classification of these returns is inherently probabilistic. Applying a traditional NeRF training routine can result in the network learning “phantom surfaces” in free space between conflicting range measurements, similar to how “floater” aberrations may be produced by an image model. We show that by formulating loss as an integral of probability (rather than as an integral of optical density) the network can learn multiple peaks for a given ray, allowing the sampling of first, nth, or strongest returns from a single output channel.
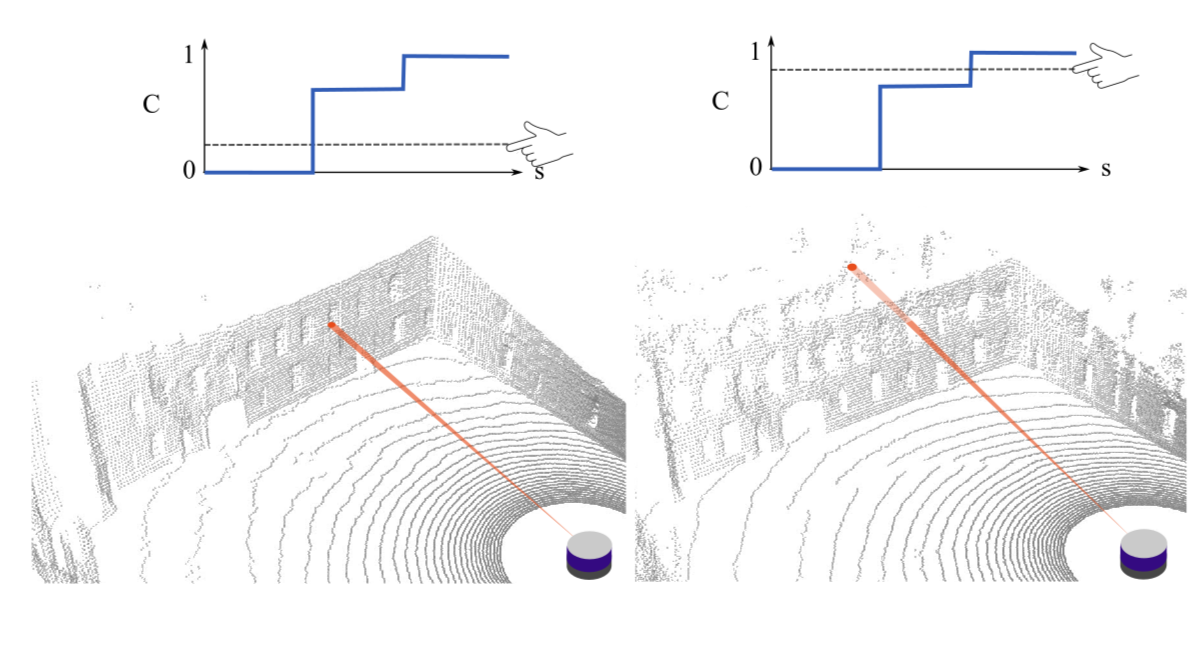
PLINK can be used to generate high quality synthetic LiDAR scans from previously unvisited locations. In the demo below, given a noisy trajectory of raw data (left), PLINK is able to accurately produce new LiDAR scans along an arbitrary sensor trajectory within that space (right). PLINK is particularly well suited for handling unstructured and noisy environments with porous and partially reflective surfaces.
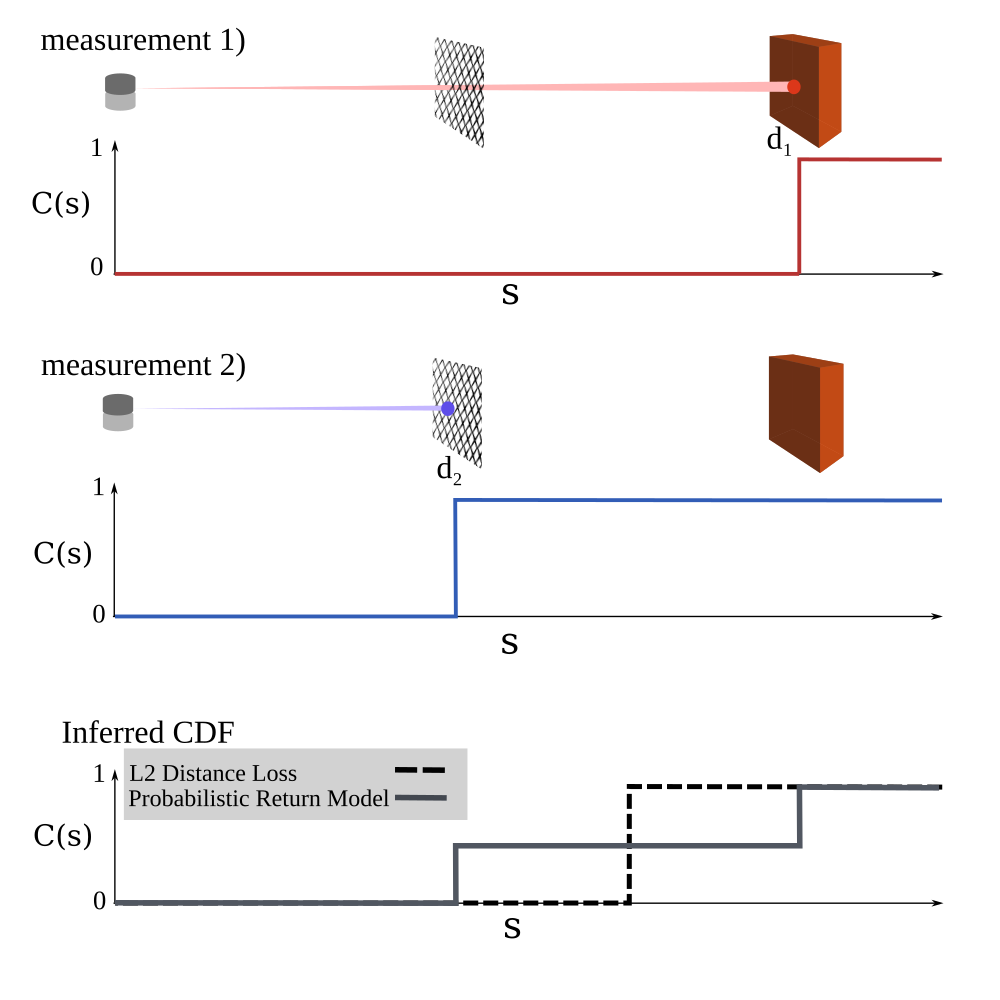
Consecutive pulses from a static LiDAR sensor should in theory return the same range measurement every time. In practice, the interplay of semi-transparent surfaces, beam divergence, fluttering of loose foliage, discretization effects, and high sensitivity at sharp corners inevitably introduces a level of stochasticity into recorded data. PLiNK rexamines the process through which a NeRF can be trained from LiDAR data in order to reconcile this difference from deterministic RGB data.
Because 3D structure is learned indirectly when training off image data, "floater" artifacts are produced in situations where degenerate geometry under-constrains the multi-view reconstruction problem. Training directly on depth information from LiDAR data alleviates this ambiguity, however, conflicting LiDAR data over-constrains the problem, introducing another kind of "phantom surface" as shown below. Attempting to directly optimize conflicting depth measurements using the traditional NeRF L2 loss regime will cause the network to learn phantom surfaces at compromise locations.